C# .NET - The beginning

Today I integrate C# in this blog. I also will write in English to improve my language skills and to reach a bigger audience. :)

I started using C# months ago and will learning a lot more because it is widely spread also in my company. C# is a very powerful tool with a huge .NET-library.

I also write this blog because I think, that I can learn much from the comments here.

Greetings,
Steffen

Python 054 A moving snake which doesn't touch itself

When the snake is moving, it checks if there are some body parts in front of the snake.

Code with indentation:
http://pastebin.com/Kh67858f

Python 053 Outer space snakes

Python 052

Last year I already make a programm for calculating magnetic fields of wires and coils. This one here is a slightly better version. :)




# Calculation of a magnetic field of a wire

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
from visual import *

# constant
I = 1
mu0 = 1e-7
constant = mu0/(4*np.pi)

# coil
parts = 238
coord2 =[]
ball = []
size = 25
factor = 6.0
steigung = 0.3
for i in range(parts):
coord2.append((size*(sin(i/factor)),size*(cos(i/factor)),steigung*i))
ball.append(sphere(pos=(coord2[i][0],coord2[i][1],coord2[i][2])))

# calculate the b-field
def bfield(x,y,z):
b = 0
for i in range(parts-1):
dlx = coord2[i+1][0]-coord2[i][0]
dly = coord2[i+1][1]-coord2[i][1]
dlz = coord2[i+1][2]-coord2[i][2]
dl = np.array([dlx,dly,dlz])
rspace_minus_rwire_x = x - (coord2[i][0]+dlx)
rspace_minus_rwire_y = y - (coord2[i][1]+dly)
rspace_minus_rwire_z = z - (coord2[i][2]+dlz)
rspace_minus_rwire = np.array([rspace_minus_rwire_x, rspace_minus_rwire_y, rspace_minus_rwire_z])
absr = (rspace_minus_rwire_x**2 + rspace_minus_rwire_y**2 + rspace_minus_rwire_z**2)**0.5
a = constant * I * np.cross(dl, rspace_minus_rwire) / absr**3
#b += (a[0]**2 + a[1]**2 + a[2]**2)**0.5
b += a
return b

# visualisation
for x in range(-42,42,3):
for z in range(-60,40,6):
y = 0
a = bfield(x,y,z)
a = 800000000 * a
#print a
limit = 10 # largest arrow size
if abs(a[0]) > limit or abs(a[1]) > limit or abs(a[2]) > limit:
a = (0,0,0)
arrow(pos=(x,y,z),axis=(a), color=color.green)

Here is the code with indentation:
http://paste.pocoo.org/show/338355/

Python 051 Magnetic field of a wire using Biot-Savart-law

This programm doesn't use numpy. Therefore I recommend to use it for smaller calculations.



Code with indentation:
http://paste.pocoo.org/show/337101/

Python 050 Test-charge between other charged bodies

Here you will find the code:
http://paste.pocoo.org/show/273774/

Python 049 Laplace-algorithm for calculating voltage between different potentials numerically

The white edges have a potential of 0 V. The two bodies inside have a potential of 30 V. The voltage in the space between has been calculated numerically with the laplace-algorithm.

from visual import *

ball = []
v = [] # v = voltage
vnew = [] # new calculated voltage
unchangeableflag = [] # if 1 --> value cannot be changed
size = 35 # size of the field
scene.center = (size/2, size/2, 0)
vmax = 100.0

# initalize
for n in range(size*size+size+1):
v.append(0)
vnew.append(0)
unchangeableflag.append(0)

# draw raster
for x in range(size):
for y in range(size):
ball.append([]) # x-pos, y-pos
ball[x*size+y] = sphere(pos=(x,y), radius = 0.4)

# set unchangeable potentials
for n in range(size):
v[n] = 0.0
unchangeableflag[n] = 1

for n in range(size):
v[n*size-1] = 0.0
unchangeableflag[n*size-1] = 1

for n in range(size):
v[n*size] = 0.0
unchangeableflag[n*size] = 1

for n in range(size):
v[size*size-size+n] = 0.0
unchangeableflag[size*size-size+n] = 1

v[250] = vmax
unchangeableflag[250] = 1
v[475] = vmax
unchangeableflag[475] = 1
print "set unchangeable potentials!"

# laplace-algorithm
for a in range(1000000):
for x in range(size):
for y in range(size):
if x % size != 1:
pass
if x % size != size - 1:
pass
if y % size != 1:
pass
if y % size != size - 1:
pass
if unchangeableflag[x*size+y] == 0:
vnew[x*size+y] = (v[(x+1)*size+y] + v[(x-1)*size+y] + v[x*size+y+1] + v[x*size+y-1]) / 4.0

# vnew --> v
colorfactor = 10.0
for x in range(size):
for y in range(size):
if unchangeableflag[x*size+y] == 0:
v[x*size+y] = vnew[x*size+y]
ball[x*size+y].color = (v[x*size+y]/10,0.2,0.2)
if v[x*size+y] >= 0.2 * vmax:
ball[x*size+y].color = ((abs(v[x*size+y]/colorfactor/5.0)),0,0)
else:
ball[x*size+y].color = (0,0,(abs(v[x*size+y]/colorfactor)))

Code with identation:

http://paste.pocoo.org/show/218999/

Python 048 Objects with a minimal distance and a path between them

# date: 20100520
# object that have a minimal distance between them
# using faster algorithm with the filter-function
# building a path between close objects

import random
from visual import *

Ncell = 4000
cell = [[10,10]] # first cell is given
ball = sphere(pos=(10,10))
size = Ncell/15 # size of the field
scene.center = (size/2, size/2, 0)
min_dist = 5 # minimal distance between two bodies
path_dist = min_dist*1.5 # draw a path if length is path-dist or shorter

for i in range(Ncell):
x = random.randint(1,size)
y = random.randint(1,size)
far = 1
# coarse filter
cell2 = filter(lambda k: abs(k[0] - x) < min_dist and abs(k[1] - y) < min_dist , cell) # excellent :)
# fine filter
for i in range(len(cell2)):
r = ((x-cell2[i][0])**2 + (y-cell2[i][1])**2)**0.5
if r < min_dist:
far = 0
pass
if far == 1:
cell.append([x,y]) # x-pos, y-pos
ball = sphere(pos=(x,y))

# building the path between two objects
for i in range(len(cell)):
# coarse filter
cell2 = filter(lambda k: abs(k[0] - cell[i][0]) < path_dist and abs(k[1] - cell[i][1]) < path_dist , cell)
# fine filter
for j in range(len(cell2)):
r = ((cell[i][0]-cell2[j][0])**2 + (cell[i][1]-cell2[j][1])**2)**0.5
if r < path_dist:
curve(pos=([cell[i][0],cell[i][1]],[cell2[j][0],cell2[j][1]]))


Here is the code with indentation
http://paste.pocoo.org/show/216285/

Python 047 pyprocessing + mouseevent + color

#You can easily use mouse-events in pyprocessing. Here I combine mouse position with a RGB-color-value.

from pyprocessing import *

size(900,600)
background(1, 1, 1)
strokeWeight(6)
x1 = 0
y1 = 0
x2 = 0
y2 = 0
x = [0,0,0]
y = [0,0,0]

def draw():
if mouse.pressed:
x1 = mouse.x
y1 = mouse.y
if mouse.pressed:
x2 = pmouse.x
y2 = pmouse.y
stroke(x1,y1,1)
line(x1, y1, x2, y2)
run()

Here is the code with identation:
http://bit.ly/c4QD2o

Python 046 Artifical Life :)

The eyes move from left to right and back.
And the arm are waving around. (at least in my version)

#artifical intelligence
#shiranutachi = an other form of live :)

from visual import *
import numpy as np
import time
from random import randint

N = 7 #number of shiranu
size = 3*N
Shiranu = []
leg1 = []
leg2 = []
arm1 = []
arm2 = []
eye1 = []
eye2 = []
eye1black = []
eye2black = []
arm1angle = []
arm2angle = []
xx = []
yy = []
zz = []
scene.center = (size/2.0, 0, size/2.0)

colors = [color.green, color.yellow, color.blue, color.red]

#instantiation
for i in range(N):
x = random.randint(0, size)
y = 0
z = random.randint(0, size)
print (x,y)
Shiranu = Shiranu + [sphere(pos=(x,y,z), radius=1, color=colors[i % 4])]
leg1 = leg1 + [curve(pos=[(x-0.5,y,z),(x-0.5,y-1.6,z)], color=colors[i % 4], radius=0.1)]
leg2 = leg2 + [curve(pos=[(x+0.5,y,z),(x+0.5,y-1.6,z)], color=colors[i % 4], radius=0.1)]
arm1 = arm1 + [curve(pos=[(x-0.95,y,z),(x-1.5,y+0.6,z)], color=colors[i % 4], radius=0.1)]
arm2 = arm2 + [curve(pos=[(x+0.95,y,z),(x+1.5,y+0.6,z)], color=colors[i % 4], radius=0.1)]
eye1 = eye1 + [sphere(pos=(x-0.40,y+0.1,z+0.67), radius=0.3, color=color.white)]
eye2 = eye2 + [sphere(pos=(x+0.40,y+0.1,z+0.67), radius=0.3, color=color.white)]
eye1black = eye1black + [sphere(pos=(x-0.45,y+0.1,z+0.90), radius=0.1, color=color.black)]
eye2black = eye2black + [sphere(pos=(x+0.45,y+0.1,z+0.90), radius=0.1, color=color.black)]
xx = xx + [x]
yy = yy + [y]
zz = zz + [z]

#motion
t = 0
dt = 0.1 #better not change
while t<3000:
t += dt
#todo: armmovement isnt ready
if t % 3.1415 > 2.0:
arm1angle = radians(t)
if t % 3.1415 < 1.0:
arm1angle = radians(-t)
else:
pass
print arm1angle
for i in range(N):
eye1black[i].pos.x = eye1black[i].pos.x + cos(t+i/1)/180 #this is for eye-movement
eye2black[i].pos.x = eye2black[i].pos.x + cos(t+i/1)/180
#todo: armmovement isnt ready
arm1[i].pos[0] = (xx[i]-0.95,yy[i],zz[i])
arm1[i].pos[1] = (xx[i]-0.95+cos(arm1angle)*1, yy[i]+sin(arm1angle)*1, zz[i])
if 200 > degrees(arm1angle) > 90:
pass
else:
arm2[i].pos[0] = (xx[i]+0.95,yy[i],zz[i])
arm2[i].pos[1] = (xx[i]+0.95+cos(arm1angle)*1, yy[i]+sin(arm1angle)*1, zz[i])
time.sleep(0.001)

Python 045 Lorentz force

import time
from visual import *
# lorentzkraft

scene.title="..."
scene.width=600
scene.height=600
scene.autoscale = 0
scene.forward = (-1,-.5,-1)
R = 0.1

avector = [2,1,2]
bvector = [1,0,0]
cvector = cross(avector,bvector)

a = arrow(pos=(0,0,0), axis=avector, shaftwidth=R, color=color.white)
b = arrow(pos=(0,0,0), axis=bvector, shaftwidth=R, color=crayola.green)
c = arrow(pos=(0,0,0), axis=cvector, shaftwidth=R, color=crayola.yellow)

alabel=label(pos=avector, text="dl", yoffset=-5, opacity=0, box=0, line=0)
blabel=label(pos=bvector, text="B", yoffset=-5, opacity=0, box=0, line=0)
clabel=label(pos=cvector, text="F", yoffset=-5, opacity=0, box=0, line=0)

line1 = sphere(radius=0.01)
line1.trail = curve()
line2 = sphere(radius=0.01)
line2.trail = curve()

size = .1
for n in range(3000):
avectorold = avector
cvectorold = cvector

avector[0] = sin(n/10.0*size)
a.axis.x = avector[0]
avector[1] = sin(n/10.0*size*1.83)
a.axis.y = avector[1]
avector[2] = sin(n/10.0*size*1.33)
a.axis.z = avector[2]

cvector = cross(avector,bvector)
c.axis = cvector

#LABEL
alabel.pos = avector
blabel.pos = bvector
clabel.pos = cvector
alabel.text = "dl: " + str(avector)
blabel.text = "B: " + str(bvector)
clabel.text = "F: " + str(cvector)

#TRAIL
line1.trail.append(pos=avector)
line2.trail.append(pos=cvector, color=color.yellow)
time.sleep(0.1)

Python 044 Charges

#coulomb force 2-dimensional
#visualised with vpython-spheres
#strongest field = color red
#lowest field = color blue

from visual import sphere, scene
from numpy import log
scene.center = (25,25,0)

charge = [ #posx, posy, charge
[20.01, 20.01, 1],
#[15, 0.01, -3],
[20.01, 25.21, -1]
]

#compute the field strength
const = 8.988*10**9 #Vm/As
def field(posxtest,posytest,posx,posy,charge):
dx = abs(posxtest-posx)
dy = abs(posytest-posy)
r = (dx**2+dy**2)**(0.5)
E = const * charge / r
return E

posxtest = range(1,70)
posytest = range(1,40)

for x in posxtest:
for y in posytest:
e = 0
for elem in charge: #ok
e += field(x,y,elem[0],elem[1],elem[2])
colorfactor = 2000000000
#print e/colorfactor
ball = sphere(pos=[x,y],radius=0.7)
if e >= 0:
ball.color = [(e/colorfactor),0,0]
if e < 0:
ball.color = [0,0,(abs(e/colorfactor))]

Python 043 Matplotlib + random + select

import numpy as np
import scipy
from scipy import *
import matplotlib.pyplot as plt

x = np.random.randint(0, 10, 10000)
x = x.reshape(100,100)

a = select([x > 8, x > 7],[x,x+10])

plt.imshow(a)
plt.show()

Python 042 Ball springt durchs Gelände

from visual import *
from math import *
import numpy as np
import time

scene.center=(10,0,5)

l = 2.5
#coordinate system
curve(pos=[(-l/2,0,0),(2*l,0,0)],radius=0.05,color=color.green)
curve(pos=[(0,-l/2,0),(0,2*l,0)],radius=0.05,color=color.blue)
curve(pos=[(0,0,-l/2),(0,0,2*l)],radius=0.05,color=color.red)

xwidth=40
zwidth=40
ebene = []
normal = []

#ground surface
for x in range(xwidth):
ebene.append([])
normal.append([])
for z in range(zwidth):
ebene[x].append(sin(x/4.0)+sin(z/4.0)) #FUNCTION
normal[x].append(0)

#draw ground surface
for x in range(xwidth-1):
for z in range(zwidth-1):
curve(pos=[(x,ebene[x][z],z),(x+1,ebene[x+1][z],z)],radius=.1,color=color.green)
curve(pos=[(x,ebene[x][z],z),(x,ebene[x][z+1],z+1)],radius=.1,color=color.green)

#ball
ball = sphere(pos=(8,4,11),radius=.3)
vektor = [-0,-0.02,-0]
ball.trail = curve(color=ball.color, radius=.1)

#calculate surface normal
def surfacenormal(pointx,pointz):
pointy = sin(pointx/4.0)+sin(pointz/4.0) #FUNCTION
start = (pointx,pointy,pointz)
#derivative and cross product of fw and fu
fu = np.array([1,0.25*cos(pointx/4.0),0]) #FUNCTION
fw = np.array([0,0.25*cos(pointz/4.0),1]) #FUNCTION
fv = np.cross(fw,fu)
end = (fv[0]+pointx,fv[1]+pointy,fv[2]+pointz)
normal = curve(pos=[start, end])
return normal.pos

t=0
veca = [0,0,0]
vecc = [0,0,0]
#movement
while 1:
t += 1
ball.pos = ball.pos + vektor
ball.trail.append(pos=ball.pos)
if (ball.pos.y <= (sin(int(ball.pos.x/4.0))+sin(int(ball.pos.z/4.0)))): #FUNCTION
veca[0] = -vektor[0] #incoming vector
veca[1] = -vektor[1]
veca[2] = -vektor[2]
vecb = surfacenormal(int(ball.pos.x),int(ball.pos.z)) #surface normal
vecc[0] = vecb[1][0]-vecb[0][0]
vecc[1] = vecb[1][1]-vecb[0][1]
vecc[2] = vecb[1][2]-vecb[0][2]
vecref = 2*norm(vecc)-norm(veca)
vektor = vecref * mag(veca)

vektor[1]=(vektor[1]-0.0001)*0.999 #Daempfung (vereinfacht)
time.sleep(.001)

Python 041 Winkel zwischen landender Kugel und Oberflächennormale

Das Programm gibt den Winkel an der zwischen dem Vektor einer auf den Boden fallenden Kugel und der Oberflächennormale liegt.

from visual import curve, scene, sphere, color, array
from math import *
import numpy as np
import time

scene.center=(10,0,5)

l = 2.5
#coordinate system
curve(pos=[(-l/2,0,0),(2*l,0,0)],radius=0.05,color=color.green)
curve(pos=[(0,-l/2,0),(0,2*l,0)],radius=0.05,color=color.blue)
curve(pos=[(0,0,-l/2),(0,0,2*l)],radius=0.05,color=color.red)

xwidth=22
zwidth=11
ebene = []
normal = []

#ground surface
for x in range(xwidth):
ebene.append([])
normal.append([])
for z in range(zwidth):
ebene[x].append(sin(x/4.0)+sin(z/4.0)) #FUNCTION
normal[x].append(0)

#draw ground surface
for x in range(xwidth-1):
for z in range(zwidth-1):
curve(pos=[(x,ebene[x][z],z),(x+1,ebene[x+1][z],z)],radius=.1,color=color.green)
curve(pos=[(x,ebene[x][z],z),(x,ebene[x][z+1],z+1)],radius=.1,color=color.green)

#ball
ball = sphere(pos=(10,5,5),radius=.3)
vektor = [-0,-0.02,-0]

#calculate surface normal
def surfacenormal(pointx,pointz):
pointy = sin(pointx/4.0)+sin(pointz/4.0) #FUNCTION
start = (pointx,pointy,pointz)
#derivative and cross product of fw and fu
fu = np.array([1,0.25*cos(pointx/4.0),0]) #FUNCTION
fw = np.array([0,0.25*cos(pointz/4.0),1]) #FUNCTION
fv = np.cross(fw,fu)
end = (fv[0]+pointx,fv[1]+pointy,fv[2]+pointz)
normal = curve(pos=[start, end])
#print(normal.pos)
return normal.pos

t=0
veca = [0,0,0]
vecc = [0,0,0]
#movement
while 1:
t += 1
ball.pos = ball.pos + vektor
if (ball.pos.y <= (sin(int(ball.pos.x/4.0))+sin(int(ball.pos.z/4.0)))): #FUNCTION #maybe round()
veca[0] = -vektor[0] #incoming vector
veca[1] = -vektor[1]
veca[2] = -vektor[2]
vecb = surfacenormal(int(ball.pos.x),int(ball.pos.z)) #surface normal
vecc[0] = vecb[1][0]-vecb[0][0]
vecc[1] = vecb[1][1]-vecb[0][1]
vecc[2] = vecb[1][2]-vecb[0][2]
zaehler = veca[0]*vecc[0]+veca[1]*vecc[1]+veca[2]*vecc[2]
nenner = (np.sqrt((veca[0])**2+(veca[1])**2+(veca[2])**2)*np.sqrt((vecc[0])**2+(vecc[1])**2+(vecc[2])**2))
cosalpha = zaehler/nenner
alpha = np.arccos(cosalpha)
winkel = np.degrees(alpha)
print(winkel)

time.sleep(.01)

Python 040 Normalenvektoren einer Fläche / surface normals

from visual import curve, scene, sphere, color, array
from math import *
xwidth=22
zwidth=11
ebene = []
for x in range(xwidth):
ebene.append([])
for z in range(zwidth):
ebene[x].append(sin(x/4.0)+sin(z/4.0)) #FUNCTION
for x in range(xwidth-1):
for z in range(zwidth-1):
curve(pos=[(x,ebene[x][z],z),(x+1,ebene[x+1][z],z)],radius=.1,color=color.green)
curve(pos=[(x,ebene[x][z],z),(x,ebene[x][z+1],z+1)],radius=.1,color=color.green)
for i in range(xwidth):
pointx = i
for j in range(zwidth):
pointz = j
pointy = sin(pointx/4.0)+sin(pointz/4.0) #FUNCTION
start = (pointx,pointy,pointz)
#derivative
fu = [1,0.25*cos(pointx/4.0),0] #FUNCTION
fw = [0,0.25*cos(pointz/4.0),1] #FUNCTION
fv = [0,0,0] #will change next line
#cross product of fw and fu
fv[0] = fw[1]*fu[2]-fu[1]*fw[2]
fv[1] = fw[2]*fu[0]-fu[2]*fw[0]
fv[2] = fw[0]*fu[1]-fu[0]*fw[1]
end = (fv[0]+pointx,fv[1]+pointy,fv[2]+pointz)
normal = curve(pos=[start, end])

Python 039: Partielle Ableitung bzw. Gradient

from sympy import *
import numpy

x = Symbol('x')
y = Symbol('y')
gleichung = x**2+y**2
xx = diff(gleichung, x)
yy = diff(gleichung, y)

vektor = numpy.array((xx, yy))
print vektor

x = 1
y = 1

print(xx.evalf)

Python 038: Faltung einer Dreiecksfunktion mit einer Rechteckfunktion

from numpy import *
from pylab import *
#print convolve.__doc__
#a = arange(12)
a = [0,0,0,1,2,3,4,5,6,7,8,7,6,5,4,3,2,1,0,0,0] #Dreieck
b = [0,0,0,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,0,0,0]
h = convolve(a,b,mode=0)
i = convolve(a,b,mode=1)
#j = convolve(a,b,mode=2)
print(h)
print(i)
#print(j)
plot(i)
hold(True)
#plot(j)
grid(True)
show()

Python 037

schmalere Streifen, welche auf den andern Ball zeigen

from visual import *

ball1 = sphere()
ball1.pos = (3,0,0)
ball2 = sphere()
ball2.pos = (0,0,0)
ball2.color = color.green
ball3 = sphere()
ball3.pos = (-3,0,0)
ball3.color = color.cyan

size = 20
t=0
while(1):
rate(10)
t += 1
ball1.pos.x = size*sin(t/10.0)
ball1.pos.y = size*sin(t/20.0)
ball1.pos.z = size*sin(t/30.0)
ball3.pos.x = size*cos(t/10.0)
ball3.pos.y = size*sin(t/20.0)
ball3.pos.z = size*sin(t/30.0)
tail1 = curve(pos=(ball1.pos,(1*ball3.pos+5.0*ball1.pos)/6.0))
tail1.radius = 0.2

Python 036

from visual import *

ball1 = sphere()
ball1.pos = (3,0,0)
ball2 = sphere()
ball2.pos = (0,0,0)
ball2.color = color.green
ball3 = sphere()
ball3.pos = (-3,0,0)
ball3.color = color.cyan

size = 10
t=0
while(1):
rate(30)
t += 1
ball1.pos.x = size*cos(t/50.0)
ball1.pos.y = size*sin(t/50.0)
ball3.pos.x = size*(-cos(t/30.0))
ball3.pos.z = size*(-sin(t/30.0))
tail1 = curve(pos=(ball1.pos,((1*ball3.pos)+(0.3*ball1.pos))))

Python 035

from visual import *

ball1 = sphere()
ball1.pos = (3,0,0)
ball2 = sphere()
ball2.pos = (0,0,0)
ball2.color = color.green
ball3 = sphere()
ball3.pos = (-3,0,0)
ball3.color = color.cyan

size = 10
t=0
while(1):
rate(30)
t += 1
ball1.pos.x = size*cos(t/20.0)
ball1.pos.y = size*sin(t/20.0)
ball3.pos.x = size*(-cos(t/20.0))
ball3.pos.z = size*(-sin(t/20.0))
tail1 = curve(pos=(ball1.pos,ball3.pos))

Python 034

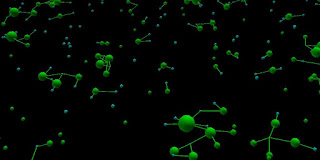
Ich habe jetzt eine künstliche Welt erstellt. Die grünen Kugeln stellen Zellen dar. Die blauen Kugeln stellen Wasser dar. Wenn die Zellen dicht am Wasser liegen, werden Versorgungsarme aufgebaut. Die Zelle wächst und der Wasseranteil wird kleiner.

from visual import *
import random

scene.width=400
scene.height=700

arrayx = 300
arrayy = 300
anzahlzellen = arrayx
anzahlwasser = arrayx
scene.center=(arrayx/2,arrayy/2,0)

t=0
zelle = []
wasser = []
verbindung = []
for x in range(arrayx):
for y in range(arrayy):
zelle.append(0)
wasser.append(0)
verbindung.append(0)

def zufall():
ax = random.random()
ay = random.random()
ax = ax * arrayx
ay = ay * arrayy
ort =(ax,ay)
return ort

for i in range(anzahlzellen):
ort = zufall()
zelle[i+1] = sphere(pos=(ort), color=(.0,.9,.0))

for i in range(anzahlwasser):
ort = zufall()
wasser[i+1] = sphere(pos=(ort), color=(.0,.9,.9))

for i in range(anzahlzellen):
for j in range(anzahlwasser):
abstand = sqrt(((zelle[i+1].pos[0]-wasser[j+1].pos[0])**2) + ((zelle[i+1].pos[1]-wasser[j+1].pos[1])**2))
if abstand <= 11:
verbindung[i*arrayx+j] = curve(pos=[(zelle[i+1].pos[0],zelle[i+1].pos[1]),(wasser[j+1].pos[0],wasser[j+1].pos[1])], radius=.2, color=color.green)
#if verbindung.pos != (0,0,0):
zelle[i+1].radius += .5
wasser[j+1].radius -= .2

Matlab 006

clear all; clc;
N = 80;
I = zeros(N,N);
kN = linspace(1,N,N);
[x,y] = meshgrid(kN);
size = .5;
A0 = N/2; B0 = N/2; % A=B = Kreis % Halbachsen
x0 = N/2; % Mitte im Feld
y0 = N/2;
F0 = ( ((x-x0)/A0).^2 + ((y-y0)/B0).^2 <= size);
abstand = (sqrt((x-x0).^2 + (y-y0).^2)).^2;
var =130;
F1 = exp(-(abstand-var) .* (abstand-var)/20000) %gauss
surf(F1)

Python 033

Hier nochmal ein anderer, einfacherer Programmcode:

from visual import *
import random

scene.width=900
scene.height=700
scene.center=(22,11,1)

nball = 2
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

# Ball und Linie deklarieren
ball[1] = sphere(pos=(0,0,0), radius=0.0001)
ball[2] = sphere(pos=(0,0,0), radius=0.0001)
line[1] = curve(radius=1, color=color.black)

t = 0

k = 1
l = 6
m = 6
n = 1

faktor = 100
for i in range(1000):
t += 0.01
for i in range(nball):
xa = 2*sin(t)+sin(13*t)
ya = 2*cos(t)+cos(13*t)
ball[1].pos = (xa*faktor,ya*faktor,0)
line[1].append((ball[1].pos), color=color.green)

Python 032

from visual import *
import random

scene.width=900
scene.height=700
scene.center=(22,11,1)

nball = 2
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

# Ball und Linie deklarieren
ball[1] = sphere(pos=(0,0,0), radius=0.0001)
ball[2] = sphere(pos=(0,0,0), radius=0.0001)
line[1] = curve(radius=1, color=color.black)

t = 0

k = 1
l = 6
m = 6
n = 1

faktor = 100
for i in range(1000):
t += 0.01
for i in range(nball):
ball[1].pos = (sin(t*k)*faktor,cos(t*l)*faktor,0)
ball[2].pos = (sin(t*m)*faktor/1,cos(t*n)*faktor/1,0)
var = ball[1].pos + ball[2].pos
line[1].append((var), color=color.green)

Python 031

Python 030

Python 029

from visual import *
scene.width=900
scene.height=700
scene.center=(22,11,1)

abstandbaelle= 10
nballi = 8
nballj = 8
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(j*abstandbaelle,i*abstandbaelle,0), radius=1)
line[i*nballi+j] = curve(pos=[(j*abstandbaelle,i*abstandbaelle,0)], radius=1, color=color.green)

a=0
b=0
c=0
for i in range(100):
for i in range(nballi):
a += 0.03
b += 0.02
c += 0.04
for j in range(nballj):
ball[i*nballi+j].pos += (sin(a),sin(b),sin(c))
line[i*nballi+j].append((ball[i*nballi+j].pos))

Python 028

Python 027

from visual import *
scene.width=900
scene.height=700
scene.center=(1,1,1)

abstandbaelle=.001
nballi = 3
nballj = 3
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(1,j*abstandbaelle,i*abstandbaelle), radius=1)
line[i*nballi+j] = curve(pos=[(1,j*abstandbaelle,i*abstandbaelle)], radius=1, color=color.green)

a=0
for i in range(100):
for i in range(nballi):
for j in range(nballj):
a += 10
ball[i*nballi+j].pos += (sin(a),cos(a*0.231),0)
line[i*nballi+j].append((ball[i*nballi+j].pos))