Python 034

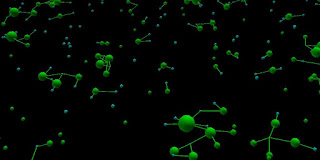
Ich habe jetzt eine künstliche Welt erstellt. Die grünen Kugeln stellen Zellen dar. Die blauen Kugeln stellen Wasser dar. Wenn die Zellen dicht am Wasser liegen, werden Versorgungsarme aufgebaut. Die Zelle wächst und der Wasseranteil wird kleiner.

from visual import *
import random

scene.width=400
scene.height=700

arrayx = 300
arrayy = 300
anzahlzellen = arrayx
anzahlwasser = arrayx
scene.center=(arrayx/2,arrayy/2,0)

t=0
zelle = []
wasser = []
verbindung = []
for x in range(arrayx):
for y in range(arrayy):
zelle.append(0)
wasser.append(0)
verbindung.append(0)

def zufall():
ax = random.random()
ay = random.random()
ax = ax * arrayx
ay = ay * arrayy
ort =(ax,ay)
return ort

for i in range(anzahlzellen):
ort = zufall()
zelle[i+1] = sphere(pos=(ort), color=(.0,.9,.0))

for i in range(anzahlwasser):
ort = zufall()
wasser[i+1] = sphere(pos=(ort), color=(.0,.9,.9))

for i in range(anzahlzellen):
for j in range(anzahlwasser):
abstand = sqrt(((zelle[i+1].pos[0]-wasser[j+1].pos[0])**2) + ((zelle[i+1].pos[1]-wasser[j+1].pos[1])**2))
if abstand <= 11:
verbindung[i*arrayx+j] = curve(pos=[(zelle[i+1].pos[0],zelle[i+1].pos[1]),(wasser[j+1].pos[0],wasser[j+1].pos[1])], radius=.2, color=color.green)
#if verbindung.pos != (0,0,0):
zelle[i+1].radius += .5
wasser[j+1].radius -= .2

Matlab 006

clear all; clc;
N = 80;
I = zeros(N,N);
kN = linspace(1,N,N);
[x,y] = meshgrid(kN);
size = .5;
A0 = N/2; B0 = N/2; % A=B = Kreis % Halbachsen
x0 = N/2; % Mitte im Feld
y0 = N/2;
F0 = ( ((x-x0)/A0).^2 + ((y-y0)/B0).^2 <= size);
abstand = (sqrt((x-x0).^2 + (y-y0).^2)).^2;
var =130;
F1 = exp(-(abstand-var) .* (abstand-var)/20000) %gauss
surf(F1)

Python 033

Hier nochmal ein anderer, einfacherer Programmcode:

from visual import *
import random

scene.width=900
scene.height=700
scene.center=(22,11,1)

nball = 2
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

# Ball und Linie deklarieren
ball[1] = sphere(pos=(0,0,0), radius=0.0001)
ball[2] = sphere(pos=(0,0,0), radius=0.0001)
line[1] = curve(radius=1, color=color.black)

t = 0

k = 1
l = 6
m = 6
n = 1

faktor = 100
for i in range(1000):
t += 0.01
for i in range(nball):
xa = 2*sin(t)+sin(13*t)
ya = 2*cos(t)+cos(13*t)
ball[1].pos = (xa*faktor,ya*faktor,0)
line[1].append((ball[1].pos), color=color.green)

Python 032

from visual import *
import random

scene.width=900
scene.height=700
scene.center=(22,11,1)

nball = 2
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

# Ball und Linie deklarieren
ball[1] = sphere(pos=(0,0,0), radius=0.0001)
ball[2] = sphere(pos=(0,0,0), radius=0.0001)
line[1] = curve(radius=1, color=color.black)

t = 0

k = 1
l = 6
m = 6
n = 1

faktor = 100
for i in range(1000):
t += 0.01
for i in range(nball):
ball[1].pos = (sin(t*k)*faktor,cos(t*l)*faktor,0)
ball[2].pos = (sin(t*m)*faktor/1,cos(t*n)*faktor/1,0)
var = ball[1].pos + ball[2].pos
line[1].append((var), color=color.green)

Python 031

Python 030

Python 029

from visual import *
scene.width=900
scene.height=700
scene.center=(22,11,1)

abstandbaelle= 10
nballi = 8
nballj = 8
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(j*abstandbaelle,i*abstandbaelle,0), radius=1)
line[i*nballi+j] = curve(pos=[(j*abstandbaelle,i*abstandbaelle,0)], radius=1, color=color.green)

a=0
b=0
c=0
for i in range(100):
for i in range(nballi):
a += 0.03
b += 0.02
c += 0.04
for j in range(nballj):
ball[i*nballi+j].pos += (sin(a),sin(b),sin(c))
line[i*nballi+j].append((ball[i*nballi+j].pos))

Python 028

Python 027

from visual import *
scene.width=900
scene.height=700
scene.center=(1,1,1)

abstandbaelle=.001
nballi = 3
nballj = 3
xvar=10000

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(1,j*abstandbaelle,i*abstandbaelle), radius=1)
line[i*nballi+j] = curve(pos=[(1,j*abstandbaelle,i*abstandbaelle)], radius=1, color=color.green)

a=0
for i in range(100):
for i in range(nballi):
for j in range(nballj):
a += 10
ball[i*nballi+j].pos += (sin(a),cos(a*0.231),0)
line[i*nballi+j].append((ball[i*nballi+j].pos))

Python 026

from visual import *
scene.width=900
scene.height=700
scene.center=(100,0,100)

abstandbaelle=.1
nballi = 20
nballj = 20
xvar=nballi*nballj

ball = []
line = []
for x in range(xvar):
ball.append(1)
line.append(1)

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(8,j*abstandbaelle,i*abstandbaelle), radius=.1)
line[i*nballi+j] = curve(pos=[(8,j*abstandbaelle,i*abstandbaelle)], radius=.3, color=(i/6,i*j/12,j/6))

for i in range(1000):
for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j].pos += sin((ball[i*nballi+j].pos)/30)
line[i*nballi+j].append((ball[i*nballi+j].pos))

Python 025

Hier wird das Magnetfeld einer Spule mit Linien dargestellt. Bei mir auf dem Bildschirm hab ich die lebendige, bzw. bewegte Variante.

Python 024

from visual import *
scene.width=900
scene.height=700
scene.center=(111,111)

abstandbaelle=.01
nballi = 6
nballj = 6
...
# hier müssen noch die Arrays deklariert werden
...

for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j] = sphere(pos=(8,j*abstandbaelle,i*abstandbaelle))
line[i*nballi+j] = curve(pos=[(8,j*abstandbaelle,i*abstandbaelle)], radius=1, color=color.green)

for i in range(100000):
for i in range(nballi):
for j in range(nballj):
ball[i*nballi+j].pos += tan((ball[i*nballi+j].pos)/3)
line[i*nballi+j].append((ball[i*nballi+j].pos))

Python 023

Das Magnetfeld einer Spule diesmal mit Python. Nur die großen Pfeile stören noch.

Python 022

from visual import *
from visual.text import *
import time
import random

x=0
xrange = 222
yrange = 222

for x in range(xrange):
for y in range (yrange):
sphere(pos=((x-xrange/2),...
y-yrange/2,0),radius=.8,color(sin(x)+.5,sin(y)+.5,sin(x*y)))

Matlab 005

Hier sieht man eine Spule. Die Helligkeitsstufen stellen den Spin eines Neutrons nach Durchqueren eines Magnetfelds dar. Je stärker das durchquerte Magnetfeld war, desto mehr Präzessionen macht der Spin des Neutrons.

Matlab 004

Hier sieht man das aufintegrierte Magnetfeld einer Spule. Am linken Rand sind die Windungen zu erkennen.

Matlab 003

Hier sieht man das Magnetfeld einer Spule mit der contourf()-Funktion dargestellt.

Matlab 002

Hier erkennt man das Magnetfeld einer Spule. Der Innenbereich ist dabei sehr homogen.

Matlab 001

Ich beschäftige mich nun schon eine ganze Weile mit Matlab und werde von nun an ein paar Programme von mir zeigen. Im Moment geht es um die Berechnung von Magnetfeldern. In der ersten Abbildung erkennt man das Magnetfeld einer Leiterschleife.

Python 021

from visual import *
from visual.text import *
import time
import random
x=0
for x in range(10000):
sphere(pos=(sin(x/3),cos(x/5),0),radius=0.3,color=(sin(x/30),sin(x/50),sin(x/70)))